0%

2021数字中国创新大赛虎符网络安全赛道

发表于 2021-04-25 更新于 2023-09-19 分类于 CTF

4月3号的比赛了，没怎么打，做了一道密码一道逆向。

因为没进线下，而且准备考研，wp没写，把草稿放博客吧。

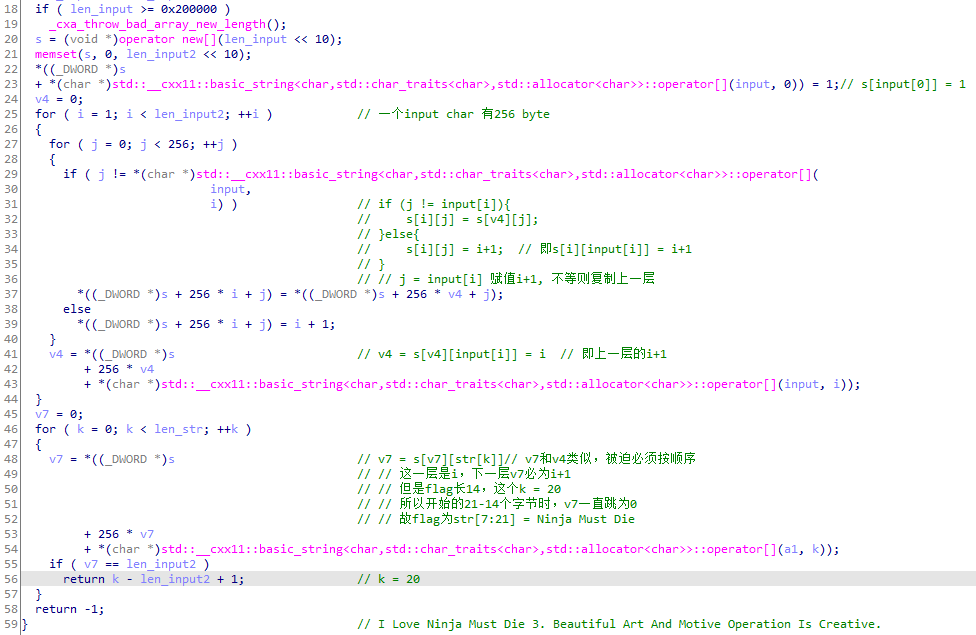
crypto 1

An interesting equation: x/(y+z)+y/(z+x)+z/(x+y)=4 x,y,z∈Z+ (mlzeng.com)

Magma Calculator (usyd.edu.au)

sage: R.<x,y,z> = QQ[];
sage: F= x**3 + y**3 + z**3 - 5 * x**2 * (y + z) - 5 * y**2 * (
....:                         z + x) - 5 * z**2 * (x + y) - 9 * x * y * z;
sage: WeierstrassForm(F)
(-14835/16, 347687/32)
sage:

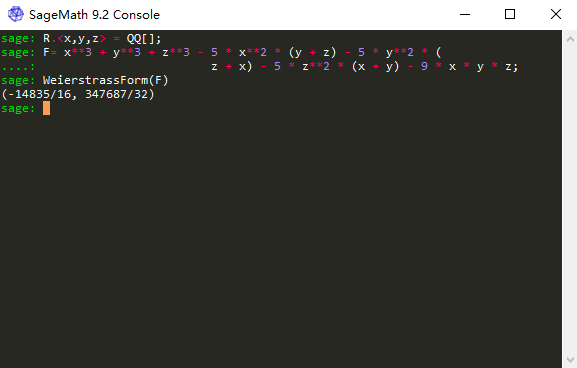
sage: E = EllipticCurve([-14835/16, 347687/32])
sage: E.rank()
1
sage: E.gens()
[(-129/4 : 85 : 1)]
sage:

(sage-sh) iyzyi@LAPTOP-1BTL2B1A:桌面$ sage ./6.sage
(-23, -7, 3)
(-8, -7, 5)
(-7, -23, 3)
(-7, -8, 5)
(-5, 7, 8)
(-5, 8, 7)
(-3, 7, 23)
(-3, 23, 7)
(-1, -1, 1)
(-1, 0, 1)
(-1, 1, 0)
(-1, 1, 1)
(0, -1, 1)
(1, -1, 0)
(1, -1, 1)
(7, -5, 8)
(7, -3, 23)
(8, -5, 7)
(23, -3, 7)
(sage-sh) iyzyi@LAPTOP-1BTL2B1A:桌面$

R<x,y,z> := RationalFunctionField(Rationals(),3); 
 
problem := ((x/(y+z) + y/(x+z) + z/(x+y)) - 6) ; 

Evaluate(problem,[-23, -7, 3]); 

problem*Denominator(problem); 

P2<x,y,z> := ProjectiveSpace(Rationals(),2); 
C := Curve(P2,x^3 - 5*x^2*y - 5*x^2*z - 5*x*y^2 - 9*x*y*z - 5*x*z^2 + y^3 - 5*y^2*z - 5*y*z^2 + z^3); 
 
Pt := C![-23, -7, 3]; 
 
E,f := EllipticCurve(C); 
 
g := f^-1; 

for n:= 1 to 100 do 
 
    nPt_inE:=n*f(Pt); 
 
    nPt_inC:=g(nPt_inE); 

    X := Numerator(nPt_inC[1]); 
    Y := Numerator(nPt_inC[2]); 
    Z := Denominator(nPt_inC[1]); 
 
printf "X=%o\nY=%o\nZ=%o\n",X,Y,Z; 
 
  if ((X gt 0) and (Y gt 0)) then 
       printf("GOT IT!!! x=apple, y=banana, z=pineapple, check the above solution\n"); 
     break; 
  else 
     printf "Nee, some coordinate was negative above, I keep in the loop\n\n"; 
  end if; 
 
end for;    
 
if Evaluate(problem, [X,Y,Z]) eq 0 then 
    printf "I evaluated the point to the original problem and yes, it worked!\n"; 
else 
    printf "Mmm this cannot happen!\n"; 
end if;

0
x^3 - 5*x^2*y - 5*x^2*z - 5*x*y^2 - 9*x*y*z - 5*x*z^2 + y^3 - 5*y^2*z - 5*y*z^2
    + z^3
X=-23
Y=-7
Z=3
Nee, some coordinate was negative above, I keep in the loop

X=-12605
Y=-26304
Z=24869
Nee, some coordinate was negative above, I keep in the loop

X=-14741015373
Y=-9962121367
Z=7010997913
Nee, some coordinate was negative above, I keep in the loop

X=-344600079128906665
Y=-423865825845143591
Z=399635339857662336
Nee, some coordinate was negative above, I keep in the loop

X=-5601501004856850884990304823
Y=-5289522737323629458801572077
Z=3709408926756435263894180473
Nee, some coordinate was negative above, I keep in the loop

X=-4070627436031293758660082617456391013440
Y=-3778570377038559830581535407335117997939
Z=3947273214056112611641932285192198633259
Nee, some coordinate was negative above, I keep in the loop

X=-1135765668330055092250323976085973407298527010733979623
Y=-1414401999299585078135301950024835142145003502627648887
Z=815923886178656038947477254264840525058302026190395683
Nee, some coordinate was negative above, I keep in the loop

X=-25281620419320048351768026986562305577512151706265133292320809015221455
Y=-16289328882340965120515308879714559149588601003364769362936593893145856
Z=23653053272182405114504253854907737996871323554596696886558694080263471
Nee, some coordinate was negative above, I keep in the loop

X=-1036283675955789870914191341173997441763288957348011417648055320105396267955\
39699048159773
Y=-2144498167749435582495047362564272898767630072564653155222059587647588025645\
15862112581047
Z=64717948697678464838747111173776757364272678503865274880411181224711461102283\
679136152793
Nee, some coordinate was negative above, I keep in the loop

X=-9210733200327079206776755372541629465472159575066558411390159130839118402437\
6586589667869747157372710541019275
Y=-2089699901380100252242640293815183679262147647927586531447673885774778272057\
8088533147052708518040528357255149
Z=89538305283456477498663693926361732820926189248425318358147867876247902898624\
183909917412197607224560490524224
Nee, some coordinate was negative above, I keep in the loop

X=12183432427029058557922642378688032230730902983101212975267528305583238455039\
10071851999217959704024280699759290559009162035102974023
Y=20260869859883222379931520298326390700152988332214525711323500132179943287700\
005601210288797153868533207131302477269470450828233936557
Z=22503240220126838668864264619424948111412000849212232184619673775885644776162\
20767789632257358521952443049813799712386367623925971447
GOT IT!!! x=apple, y=banana, z=pineapple, check the above solution
I evaluated the point to the original problem and yes, it worked!

斜杆不是分数的意思，表示不中断数据的换行。

R<x,y,z> := RationalFunctionField(Rationals(),3); 
 
problem := ((x/(y+z) + y/(x+z) + z/(x+y)) - 6) ; 

Evaluate(problem,[-3, 7, 23]); 

problem*Denominator(problem); 

P2<x,y,z> := ProjectiveSpace(Rationals(),2); 
C := Curve(P2,x^3 - 5*x^2*y - 5*x^2*z - 5*x*y^2 - 9*x*y*z - 5*x*z^2 + y^3 - 5*y^2*z - 5*y*z^2 + z^3); 
 
Pt := C![-3, 7, 23]; 
 
E,f := EllipticCurve(C); 
 
g := f^-1; 

for n:= 1 to 100 do 
 
    nPt_inE:=n*f(Pt); 
 
    nPt_inC:=g(nPt_inE); 

    X := Numerator(nPt_inC[1]); 
    Y := Numerator(nPt_inC[2]); 
    Z := Denominator(nPt_inC[1]); 
 
//printf "X=%o\nY=%o\nZ=%o\n",X,Y,Z; 
 
  if ((X gt 0) and (Y gt 0)) then 
       printf "X=%o\nY=%o\nZ=%o\n\n",X,Y,Z; 
       //printf("GOT IT!!! x=apple, y=banana, z=pineapple, check the above solution\n"); 
     //break; 
  else 
     //printf "Nee, some coordinate was negative above, I keep in the loop\n\n"; 
  end if; 
 
end for;    
 
if Evaluate(problem, [X,Y,Z]) eq 0 then 
    printf "I evaluated the point to the original problem and yes, it worked!\n"; 
else 
    printf "Mmm this cannot happen!\n"; 
end if;

reverse 1