这题真的是学到了不少。
知识点:pin插桩、idapython动调脚本、基于srop的控制流、rc4、魔改tea
菜鸡刚开始学密码学,本文如果谬误,劳请师傅们轻点骂orz~
淘宝上买了块esp8266,今天折腾了一下午,随便记录下吧。
本文转自Windows下反(反)调试技术汇总,版权归原作者所有。
对于安全研究人员来说,调试过程中经常会碰到反调试技术,原因很简单:调试可以窥视程序的运行“秘密”,而程序作者想要通过反调试手段隐藏他们的“秘密”,普通程序需要防止核心代码被调试逆向,恶意代码需要隐藏自己的恶意行为防止被跟踪。就像病毒和杀软的关系一样,为了顺利的逆向分析,有反调试手段就有对应的破解方法-反反调试。对此,天融信阿尔法实验室研究人员总结了各类常见反调试手段以及对应的绕过方案,作为总结希望与君共勉。
关于各种反调试手段,网络上和各种安全书籍上都有对应的介绍、各种调试工具插件已经集成了反调试功能,但有的只是介绍了反调试方法,并没有对应的破解方式,有的反调试手段已经失效。本文并不是研究新的反调试方法,而是对windows平台的反调试技术进行分类总结,并介绍其原理和应对方法。
合理的分类有助于学习和理解各种反调试技术的原理,由于理解不同,分类也不尽相同。当你掌握了这些技术后,可以按照自己的理解重新给它们分类。本文按照静态反调试方法与动态反调试方法将反调试技术分为两大类,其中静态反调试技术的分类原理为:程序启动时,系统会根据正常运行和调试运行分配不同的进程环境,通过检测进程环境来检测进程是否处于调试状态;根据逆向人员的工作环境和程序的正常运行环境不同,可以通过检测调试器或逆向分析工具实现反调试。动态反调试技术的分类原理是:进程运行时的执行流程是否正常、执行状态是否正常。
本文测试环境:
测试代码: https://github.com/alphaSeclab/anti-debug
调试器为原版OllyDbg1.1(http://www.ollydbg.de/odbg110.zip) 因为各种魔改带插件的OD已经自带许多反反调试功能,会影响测试效果。
测试系统为win7 SP1 32位旗舰版。
PE编辑器:LordPE
许多静态反调试技术对系统有较强的依赖,本文测试的静态反调试技术时使用的是win 7 SP1 32位旗舰版。像PEB中ProcessHeap的Flags与ForceFlags等类似反调试手段针对的是NT5.X以下版本,win7 下检测就会失效,所以本文未做介绍。
我们不一样:正常启动的进程和调试启动的进程的某些初始信息是不同的,比如进程环境块PEB、STARTUPINFO等,这些信息使用方便,经常被广泛应用于反调试技术。
PEB结构体的内容如下(部分省略):

上表中列出了Windows 7 32位SP1中PEB的结构体成员,其中我们将会介绍到的与反调试相关的成员有:偏移为0x002的BeingDebugged和偏移为0x068的NtGlobalFlag。BeingDebugged是一个标志位,就像它的名字一样,用来表示进程是否处于被调试状态,NtGlobalFlag用来表示进程的堆内存特性,调试和非调试时其值不同。所以我们只需要获取这两个值与正常状态的值比较,就能知道进程是否处于调试状态。
利用fs段寄存器指向的TEB结构可以得到PEB结构体的地址:
mov EAX,DWORD PTR FS:[0x30]
调试时该值为TRUE,非调试时该值为FALSE。所以我们可以这样判断进程是否被调试:

正常运行时,该函数返回FALSE,用OD打开调试运行时,该函数返回TRUE。
其实有一个API可以直接获取BeingDebugged的值:IsDebuggerPresent();我们看下这个API的实现代码:在OD反汇编窗口按下快捷键CTRL+G,输入函数名跳转到函数地址
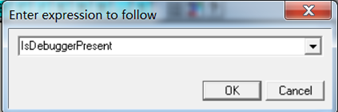

可以看到该函数其实也是读取的PEB中的BeingDebugged标志位的值。和我们的代码相比,它多了一行MOV EAX,DWORD PTRFS:[18],这行代码的作用是获取TEB的地址,我们上面说了,PEB的地址在TEB中,所以可以先获取TEB的地址,再获取PEB的地址。
破解方法:调试时手动将其置0。
OD打开被调试程序,在内存窗口CTRL+G,输入FS:[30],内存窗口将跳转到PEB的地址:
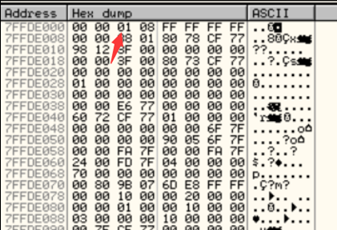
选中偏移为2的位置CTRL+E,将1改为0即可。
当进程处于调试状态时,PEB结构体偏移为0x68的NtGlobalFlag的值会被设置为0x70。所以和BeingDebugged成员检查一样,我们只需要检查其值是否为0x70就能判断程序是否被调试。

破解方法:和修改BeingDebugged的值一样,内存窗口CTRL+G输入fs:[30]跳转到PEB的地址,选中偏移0x68的地方,CTRL+E将其改为0即可。
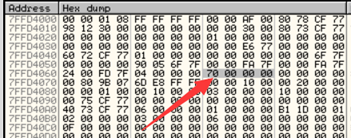
除了利用PEB查询进程相关的调试信息外,还可以利用NtQueryInformationProcess()API来获取其他各种与进程调试相关的信息。

其中第1个参数是要查询的进程的句柄值,第2个参数是要查询进程的哪些信息,该参数是一个枚举类型的值,可以查询的信息如下:

第2个参数不同的值对应于第3个参数指向不同类型的结构体,比如第2个参数填0(ProcessBasicInformation),就表示你想获取PEB的信息,然后就可以判断BeingDebugged,NtGlobalFlag的值了,和我们前面讲到的一样,但是这种实现方式稍显复杂。
这节我们主要使用该函数查询2个值:ProcessDebugPort、ProcessDebugObjectHandle,对应的枚举值为7和0x1E。
进程处于调试状态时,系统会为它分配一个调试端口,第2个参数传7时,NtQueryInformationProcess()就能获取调试端口的值,调试状态该值为0xFFFFFFFF,正常运行时该值为0。
同样,有一个API也可以检测调试端口的值:CheckRemoteDebuggerPresent()。CTRL+G定位到该函数实现部分,发现该函数其实就是内部调用了一下第2个参数为7的NtQueryInformationProcess:(实际调用的Zw版的函数,功能相同)

进程被调试时会生成调试对象,当函数的第2个参数值为0x1E(ProcessDebugObjectHandle)时就能获取调试对象句柄,正常运行时该值为0,调试运行时该值为非0值。

破解方法:如果被调试程序只是调用几次API,而不是在多个地方反复调用,我们可以在调用的时候手动修改特定参数下的调用结果:修改返回值或函数参数指向的内存。像上面的例子一样,我们可以在该函数调用结束的后手动修改参数指向的内存,修改调用结果。当函数调用传参为7/0x1E的时候,修改其第3个参数获取的值:

在call处下断,命中断点后,栈区右键,定位到第3个参数的缓冲区:
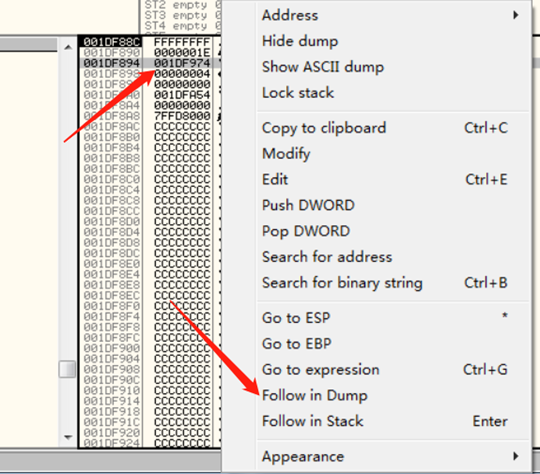
F8步过等函数调用完毕,修改第3个参数缓冲区内的值
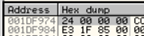
,CTRL+E,修改为0。
如果该函数在多个地方被反复调用,那么我们可以采取API HOOK的技术,修改函数内部执行代码的流程。
OD重新运行程序,反汇编区CTRL+G,输入ZwQueryInformationProcess(实际调用的是该函数),跳转到函数反汇编指令处。

第1条指令正好5个字节,我们从此处HOOK。
ALT+M查看进程的内存映射表,找到其代码区范围:
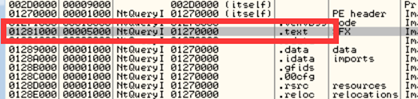
代码起始地址:0x1281000,大小为0x5000。
回到反汇编窗口ALT+C:CTRL+G跳转到0x1281000+0x4000的位置

这段空间是原程序代码区对齐用的,没有实际的代码,我们在这里实现我们的HOOK代码,将ZwQueryInformationProcess的第1条指令修改为jmp 1285000,执行HOOK代码,先判断第2个参数是不是7或0x1E,是则把第3个参数指向的缓冲区填0,直接返回,不是则执行ZwQueryInformationProcess的第1条指令mov eax,0xEA,然后跳转到ZwQueryInformationProcess第2条指令处继续执行原函数功能。
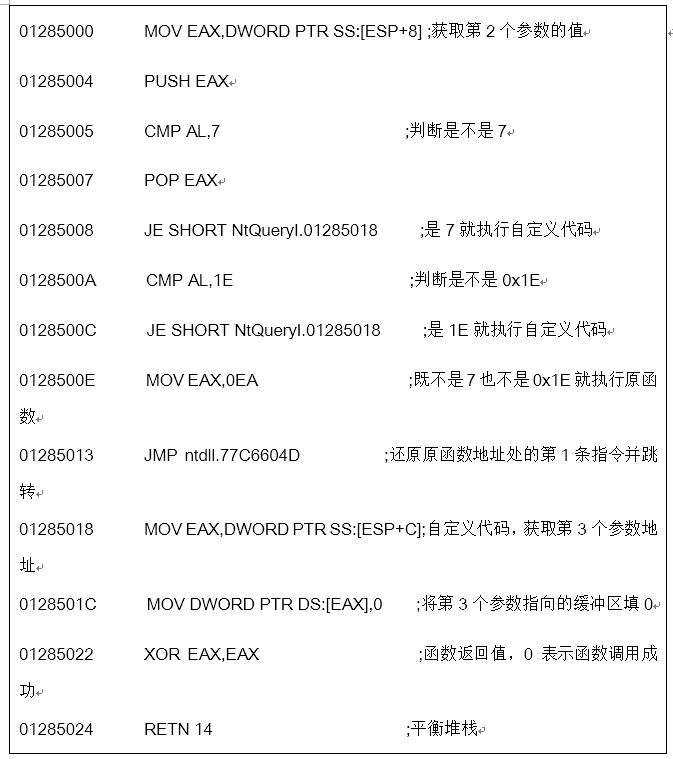
ZwQueryInformationProcess函数的两个MOV和后面的CALL RETN指令均可作为HOOK点,这里选择的第1条指令HOOK,对于这种反反调试的手段,程序可以检查API的第1个指令是不是原指令来判断是不是有HOOK代码来继续实现反调试,和动态反调试的API断点相似,后面的动态反调试会介绍怎么应对HOOK检测。
程序正常启动(双击启动)时,实际是资源浏览器通过CreateProcess()函数创建进程启动的:
 explorer启动程序时,会把倒数第2个参数STARTUPINFO结构体中的值设置为0,但调试器启动程序的时候不会,所以我们可以通过判断该结构体中的某些值是否为0来判断是否被调试:
explorer启动程序时,会把倒数第2个参数STARTUPINFO结构体中的值设置为0,但调试器启动程序的时候不会,所以我们可以通过判断该结构体中的某些值是否为0来判断是否被调试:
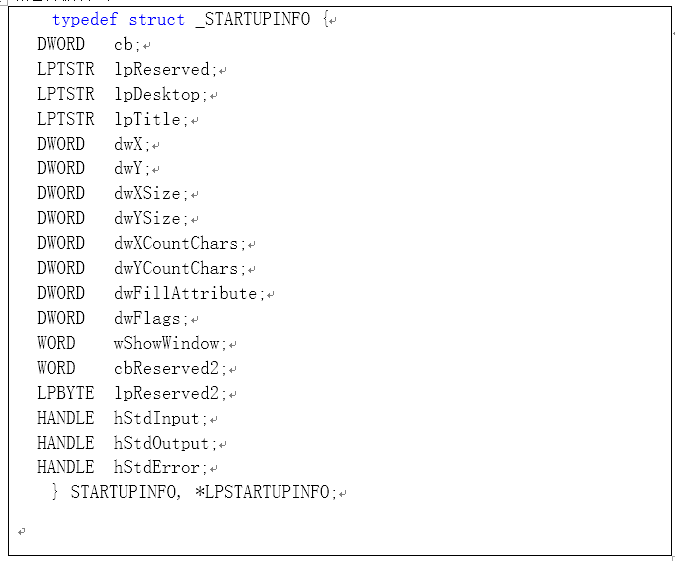 这里我们选择判断结构体中窗口坐标和大小这几个值(也可以多选几个)是否为0来实现反调试检测:
这里我们选择判断结构体中窗口坐标和大小这几个值(也可以多选几个)是否为0来实现反调试检测:

破解方法:同NtQueryInformationProcess一样,当函数调用次数较少时,可以直接修改函数调用结束后的参数值:

函数调用处下断,命中断点后,数据区定位到第1个参数指向的结构体地址,操作方法同2.1.3中修改NtQueryInfomationProcess调用结果相同。F8步过,CTRL+E修改结构体中对应的值:

当函数调用次数较多时-像NtQueryInformationProcess,我们采用的是API HOOK,那么这个函数能否使用API HOOK技术呢?我们只是修改该结构体中的部分值,而不是全部值,所以修改结构体内容要发生在函数执行完毕,所以HOOK点要选择函数将要返回时,一般这种情况是不容易HOOK的,反汇编区CTRL+G 输入GetStartupInfoW,看下GetStartupInfoW的函数实现尾部: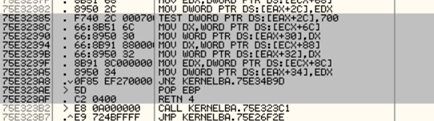
尾部POP EBP和RETN 4共4个字节,不符合我们的要求,而且返回前还有JNZ跳转另一个返回分支,不是我们期望的HOOK点。该函数实际需要填充参数指向的结构体的值,我们看下函数体中它填充的值来自哪里:
 由汇编代码实现,我们可以发现,该函数实际是先定位到PEB中偏移为0x10的_RTL_USER_PROCESS_PARAMETERS结构体(参考2.1.1中的PEB信息)地址处,然后获取参数STARTUPINFO的地址,分别将两个地址值赋值给ECX和EAX,以这两个寄存器为偏移基址,分别获取_RTL_USER_PROCESS_PARAMETERS结构体内的值,并赋值给STARTUPINFO结构体。所以,我们只需要将结构体_RTL_USER_PROCESS_PARAMETERS中的相应值置0即可实现类似API HOOK的效果。_RTL_USER_PROCESS_PARAMETERS结构体内容如下:(win7 32位SP1)
由汇编代码实现,我们可以发现,该函数实际是先定位到PEB中偏移为0x10的_RTL_USER_PROCESS_PARAMETERS结构体(参考2.1.1中的PEB信息)地址处,然后获取参数STARTUPINFO的地址,分别将两个地址值赋值给ECX和EAX,以这两个寄存器为偏移基址,分别获取_RTL_USER_PROCESS_PARAMETERS结构体内的值,并赋值给STARTUPINFO结构体。所以,我们只需要将结构体_RTL_USER_PROCESS_PARAMETERS中的相应值置0即可实现类似API HOOK的效果。_RTL_USER_PROCESS_PARAMETERS结构体内容如下:(win7 32位SP1)

STARTUPINFO的dwX、dwY、dwXSize、dwYSize分别对应该结构体中偏移为0x4C、0x50、0x54、0x58处的值,下面我们找到结构体_RTL_USER_PROCESS_PARAMETERS在内存中的位置:OD数据区CTRL+G输入FS:[0x30]定位到PEB地址,找到偏移0x10处的_RTL_USER_PROCESS_PARAMETERS地址:
0x4E1298就是我们要找的地址,数据窗口CTRL+G跳转到该地址处:
为方便我们找到那几个偏移值,数据窗口右键把数据以地址方式显示: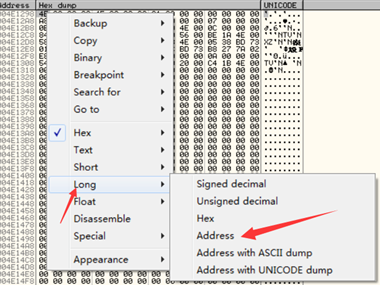
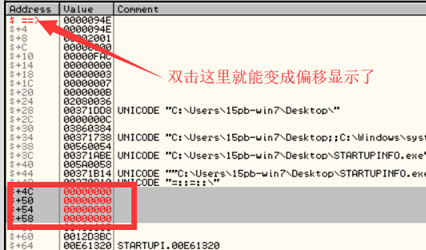
找到对应的偏移处的值,CTRL+E将其置为0即可。我们这里只比较了4个值,你也可以把结构体中其他的值置0。
一般程序正常启动时是不具备调试权限(SedebugPrivilege)的,除非自己有提权的需要主动开启,但是调试器启动程序的时候,由于调试器本身会开启调试权限,所以被调试进程会继承调试权限,因此我们可以通过检查进程是否具有调试权限来进行反调试。
检查进程是否具有调试权限的方式很简单,系统启动的时候会启动一个核心进程csrss.exe,我们可以通过判断能否使用OpenProcess打开该进程来检查当前进程是否具有调试权限,因为只有拥有管理员权限+调试权限的进程才能打开csrss.exe的句柄。严格来说这种检查方法是不太严格的,因为当进程有调试权限无管理员权限的时候也不能打开csrss.exe的句柄,幸运的是,大多数调试器都会要求提供管理员权限,所以被调试程序也会同时拥有管理员权限+调试权限。
通过CsrGetProcessId函数可以获取csrss.exe的PID,然后通过OpenProcess尝试打开csrss.exe的句柄:

破解方法:在OpenProcess函数调用上或函数起始地址下断,判断PID的值是不是csrss.exe的PID,注意:有两个csrss.exe的进程,通过任务管理器可以查看其PID的值,不要只关心一个PID。如果是这两个中的一个,直接执行到函数返回,并修改EAX的值为0即可(EAX就是函数的返回值):如下图所示(0x228 == 552)

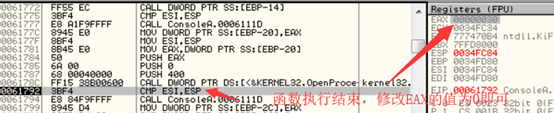
除了修改函数返回结果其实也可以直接修改查找的字符串。有的反调试程序会使用遍历进程的方式查找csrss.exe的PID值,但最终还是会调用OpenProcess,破解方式与上面相同,这里介绍另外一种破解方式:直接搜索“csrss.exe”字符串,将其缓冲区直接置0即可,这样它就找不到csrss.exe进程了:
遍历进程查找csrss.exe:
 破解方式:ALT+M转到内存窗口,右键search或快捷键ctrl+B:
破解方式:ALT+M转到内存窗口,右键search或快捷键ctrl+B: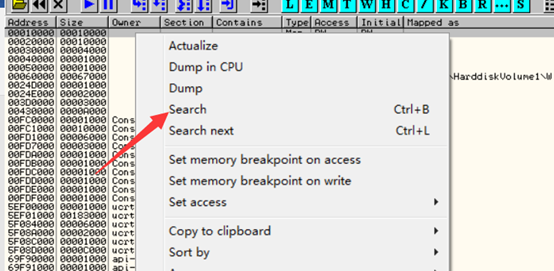
在unicode栏输入csrss(当然也有可能是asc字符串,示例代码用的是unicode)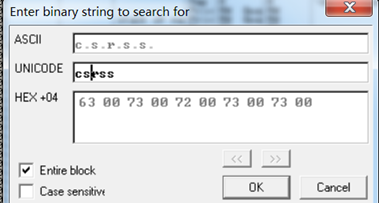
成功找到csrss.exe的字符串地址,ctrl+L继续找还有没其他地址,发现只有这一处,CTRL+E将其置0即可。
在2.1中介绍了各种进程本身状态检测的反调试技术,其原理是调试状态下的进程和正常运行时进程本身不同,这些检查是固定不变的,当所有的检查项都被我们伪装通过了之后,这些反调试手段就失效了。本节将介绍针对调试环境检测的反调试手段及反反调试手段。安全研究员要调试程序,他的工作环境和正常的工作环境是不同的,像各种分析工具、虚拟机环境等等,这些工作环境的检测就成为除进程检测外的另一种反调试手段。这时候不管进程有没有被调试,只要发现程序所处环境不正常,就认为自己被调试分析了.
当程序运行发生错误的时候,会有一个错误弹框,让用户选择关闭程序还是调试程序: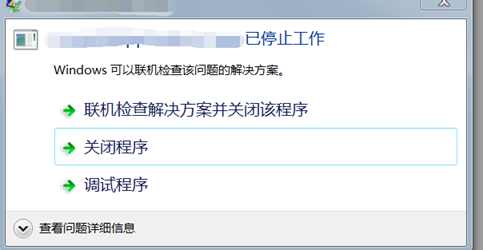
正常用户只能选择关闭程序,因为他没有调试器,对于安全研究人员则不同,他们的工作环境上搭配有对应的调试器,当程序崩溃时,他们可以选择设置好的JIT调试器调试程序。以OD举例,将OD设置为JIT调试器:Options->Just-in-time debugging: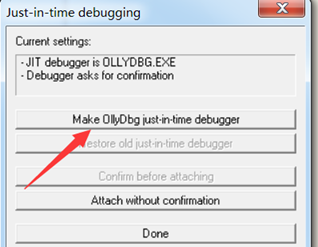
一旦设置了JIT调试器,系统就会更改注册表项中对应JIT的值:
这个注册表的位置为:
 我们可以通过查找该注册表项对应的值是否包含常用调试器的字符串来检测调试器:
我们可以通过查找该注册表项对应的值是否包含常用调试器的字符串来检测调试器:

破解方法:搜索字符串AeDebug,步骤和2.1.5相同,只是这里会搜到两个结果(一个32位路径,一个64位路径),将其全部置0即可。
窗口检测即通过查找当前系统中运行的程序窗口名称是否包含敏感程序来进行反调试。常用的函数有FindWindow、EnumWindows。FindWindow可以查找符合指定类名或窗口名的窗口句柄,EnumWindows可以枚举所有顶层窗口的句柄值,并传给回调函数。

破解方法:搜索字符串OllyDbg或OLLYDBG(你使用的调试器的类名或窗口名),将其置0即可。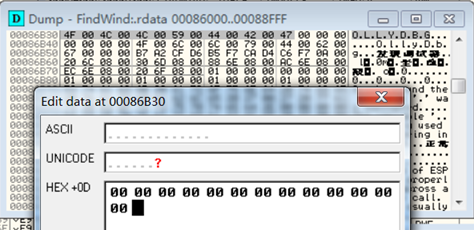
程序正常启动(双击)时,其父进程为exeplorer.exe,调试启动时其父进程为调试器,所以检查其父进程是否为explorer.exe也可以作为一个反调试手段。但是这种检测方式容易误判,因为程序也可能是由其他正常进程通过CreateProcess正常启动。NtQueryInformationProcess获取当前进程的父进程PID,通过遍历进程来获取该PID对应的进程名是否explorer.exe来实现反调试。这里还有另一种选择:获取exeplorer.exe的PID和当前进程的父进程PID比较,但是这种检测遇到一种情况会失效-系统启动两个explorer.exe,这时候会有两个explorer的PID。所以示例代码只演示比较进程名而不是比较PID。

破解方法:除了字符串搜索法外,可以选择把自己的调试器exe文件改成explorer.exe再运行,这样检测父进程名称时调试器的名称也变成explorer.exe了,另一种方法就是修改_wcsicmp/_stricmp的比较结果,让其返回0:
进程扫描是比父进程检测更暴力的检测方式:只要系统进程列表内有敏感进程,就执行反调试手段。

破解方法:最直接的还是更改调试器名称,随便换个名字即可,另一种方法就是查找字符串”OllyDbg.exe”,将其置0即可。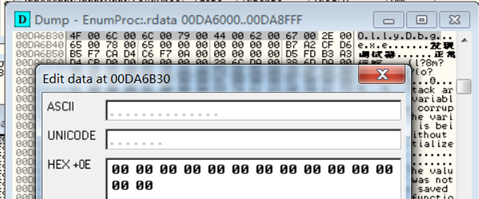
在2.1.3中我们介绍了查找调试对象句柄的方式实现反调试,其实也可以通过查找这个调试对象来实现反调试。当调试会话建立时会创建一个“DebugObject”类型的内核对象,通过遍历内核对象链表查找是否包含该类型的内核对象即可实现反调试:

破解方法:查找字符串“DebugObject”,将其置0即可。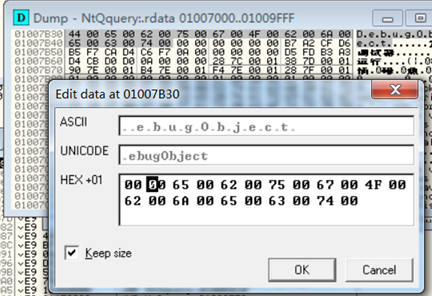
安全研究工作一般是在虚拟机环境中进行的,当进行内核调试时,虚拟机系统会处于被调试状态,VirtualKD (http://virtualkd.sysprogs.org)可以轻松实现内核调试。
当系统处于被调试状态时,我们可以通过检测该状态来实现反调试:

破解方法:系统正常启动,不开启调试模式,或开启调试模式但是不建立内核调试会话。如果有内核调试的需要,可以函数调用处下断,修改函数执行结果,或HOOK API。
这里说的调试器攻击并不是指对调试器造成破坏,而是指让调试器无法调试程序。比如ZwSetInformationThread()函数传参ThreadHideFromDebugger时,如果程序正常运行,那么该函数就相当于什么都没做,但如果程序处于被调试状态,那么该函数就可以使当前线程(一般是主线程)脱离调试器,使调试器无法继续接收该线程的调试事件,效果就像是调试器崩溃了一样:
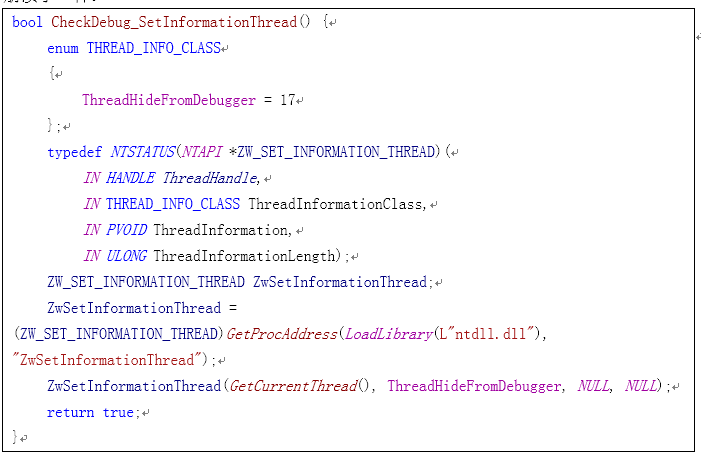
破解方式:API HOOK,当ZwSetInformationThread第2个参数为17的时候,函数直接返回。HOOK步骤参考2.1.3,HOOK代码如下:

另一种调试器攻击方式就是利用OD加载进程时的一个BUG,在PE文件格式中,数据目录表项的个数一般是0x10个,如果大于这个值,双击运行时,系统加载器会忽略这个值,但是OD加载进程时会认为PE文件格式错误,拒绝加载。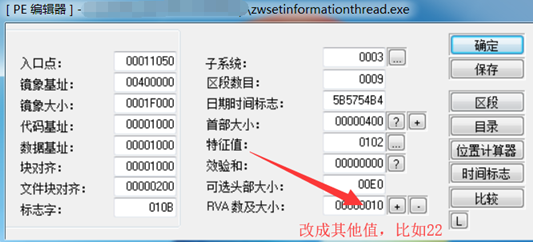
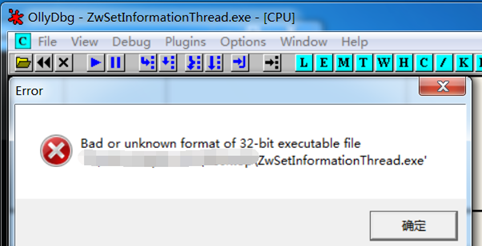 其次,双击运行系统加载器加载进程区段时,采用的是区段信息表中区段在虚拟内存中的大小和区段在文件中大小的较小值,而OD则固定采用文件大小,如果把区段在文件中的大小值改的很大,则系统加载器可以正常运行程序,而OD则会认为PE文件格式错误,拒绝加载。
其次,双击运行系统加载器加载进程区段时,采用的是区段信息表中区段在虚拟内存中的大小和区段在文件中大小的较小值,而OD则固定采用文件大小,如果把区段在文件中的大小值改的很大,则系统加载器可以正常运行程序,而OD则会认为PE文件格式错误,拒绝加载。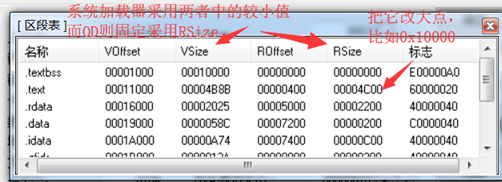
破解方法:把数据目录表改回0x10,RSize改成VSize为0x200的整数倍即可。
在第二章中介绍了基于进程状态和运行环境检测的静态反调试技术,静态反调试技术其实是对整个程序的保护,反调试手段相对“死板”,破解方式也比较简单。其实程序开发者只是想对程序的关键算法和核心数据进行保护、避免逆向分析。所以他们大多利用的是动态反调试手段:调试行为检测。
动态反调试的原理基于调试行为本身,比如,调试运行的程序比正常运行的程序执行速度慢,所以可以用时钟检测来进行反调试;遇到异常时,调试器会先接收异常事件而不是直接传递给进程本身,所以可以利用异常处理机制来实现反调试;逆向分析核心代码时需要下断点、单步跟踪等,可以检测断点、单步等实现反调试。
动态反调试的主要目的是干扰调试器,使其无法正常跟踪程序的执行流程或加大其逆向分析难度。相比静态反调试,其隐蔽性较强,技术难度更高,破解难度也更大。
程序被调试时什么事都得向调试器通知报备一下,就像是调试器的提线木偶,调试器还要和用户交互,等待用户命令再下发给程序,哪有完全自主来的爽。所以在调试器中跟踪程序代码比程序正常运行耗费的时间要多很多。时钟检测技术就是通过计算关键内容运行时间差异来判断进程是否处于被调试状态。同时程序在虚拟机中的运行速度也比正常速度慢,所以时钟检测技术一般也用于反虚拟机/反模拟器技术。计算运行时差的方式一般有两种:读取CPU时钟计数器、时间计数相关API。
x86 CPU中存在一个名为TSC(Time Stamp Counter)的64位寄存器。CPU对每个时钟周期计数,然后保存到TSC。RDTSC是一条汇编指令,用来将TSC的值读入EDX:EAX寄存器(有的程序也会使用RDTSCP汇编指令,用法相同)。
 破解方法:F9运行步过这段检测代码,如果有单步调试的需要则修改RDTSC的执行结果,把EAX,EDX置0或其他值,只要使两次RDTSC结果相同即可。
破解方法:F9运行步过这段检测代码,如果有单步调试的需要则修改RDTSC的执行结果,把EAX,EDX置0或其他值,只要使两次RDTSC结果相同即可。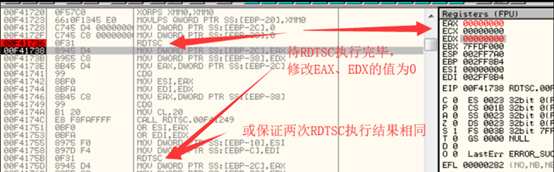
时间计数相关的API有很多,在时钟检测上RDTSC的效率和准确度相比这些API是最高的。但这些API也是一种反调试手段,这些API有:QueryPerformanceCounter、GetTickCount、GetSystemTime、GetLocalTime等,具体参考MSDN(https://docs.microsoft.com/zh-cn/windows/desktop/SysInfo/time-functions)。
这些API的使用方式大同小异,这里只介绍QueryPerformanceCounter的使用:

破解方法:改变函数调用结果,使两次获取时间相同,注意:一般这些时间API也会用于其他用途,所以除非明确知道所有的该API调用都是用来反调试,否则不要随便HOOK。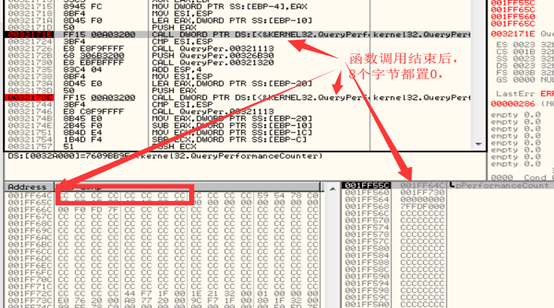
异常常用于动态反调试技术。正常运行的进程发生异常时,在SEH(Structured Exception Handling)机制的作用下,OS会接收异常,然后调用进程中注册的SEH处理。但是,若进程正被调试器调试,那么调试器就会先于SEH接收处理。利用该特征可判断进程是正常运行还是调试运行,然后根据不同的结果执行不同的操作,这就是利用异常处理机制不同的反调试原理。
Windows中的一些典型异常如下:
https://msdn.microsoft.com/zh-tw/library/aa915076.aspx

以INT3异常EXCEPTION_BREAKPOINT为例,当该异常触发时,若程序处于正常运行状态,则自动调用已经注册过的SEH;若程序处于调试运行状态,则系统会停止运行程序将控制权转给调试器。反调试程序一般会在SEH中更改程序的执行流程,若控制权交给调试器,而调试器又没有执行SEH代码,程序流程就会走向未知。
破解方法:OD调试选项中,设置忽略指定异常并传递给程序即可,意思就是这个异常不是OD设置的,是程序自己触发的,OD不处理,程序自己处理吧。分析明白异常处理逻辑后,找到异常处理更改后(如果异常处理程序更改了)的EIP,继续分析。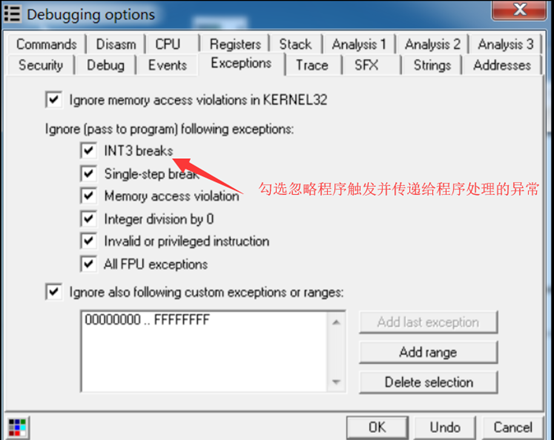
这里只是用INT3断点举例,要想主动触发其他类型的异常可以使用RaiseException()函数。这种反调试手段看似有点鸡肋,其实它的主要目的是在异常处理中改变程序的执行流程,增加逆向分析难度,除非把异常处理代码分析明白,否则就搞不懂异常处理完毕程序的新EIP在哪,从何处继续分析。而且这种把忽略异常把异常交给程序自己处理的方法并不是万能的,后面的INT 2D会“教OD做人”。
主动触发的异常可以被调试器交给程序自己处理,那么当SEH不存在,或SEH处理不了该异常的时候怎么办呢?这时候系统会调用UnhandledExceptionFilter()函数,该函数会检查进程是否处于调试状态,若是,就把异常传递给调试器,否则就弹个错误对话框,然后结束程序: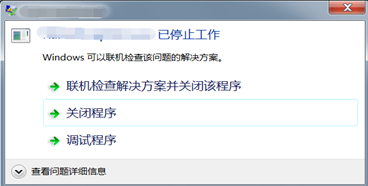
SetUnhandledExceptionFilter()可以添加一个异常处理函数来替换弹框行为,没有调试器的时候就会把异常传递给该异常处理函数去处理:
破解方法:首先像3.2.1一样要让OD把这些程序主动触发的异常忽略并交给程序处理,然后异常处理流程就走到UnhandledExceptionFilter,因为UnhandledExceptionFilter检测到没有调试器就会把异常交给SetUnhandledExceptionFilter注册的函数,而它检查有无调试器的方式就是2.1.3中提到的NtQueryInformationProcess函数第2个参数传7(ProcessDebugPort),查找调试端口。后面的处理方式就和2.1.3中一样,把NtQueryInformationProcess()函数 HOOK掉即可。
INT 2D是一个特殊的指令,原为内核模式中用来触发断点异常的,也可以在用户模式下正常运行时触发异常。但程序在OD中调试运行时有以下特点:
① 不会触发异常,只是忽略
② INT 2D的下一条指令的第一个字节会被忽略。
③ F7/F8单步命令跟踪INT 2D时,程序不会停在下条指令开始的地方,而是一直运行,直到遇到断点。
对于OD来说,忽略异常设置也没用,因为OD并没有把INT 2D当作异常,而是直接忽略。

破解方式:因为OD直接忽略INT 2D异常,所以设置忽略异常传递给程序自身处理无效,那么我们直接把INT 2D改变成OD不会忽略的异常即可,比如把它改成INT3异常。这样OD就能把异常正常传递给异常处理程序了。
在程序调试过程中,我们一般会设置许多软件断点。软件断点的原理其实就是调试器在对应设置断点的位置上修改该地址的字节为0xCC,0xCC就是x86指令中的INT 3。若是关键位置检测到该指令,即可判断进程处于调试状态。检测时要注意不是所有的位置都可以,因为0xCC既可以是INT 3指令,也可以是其他指令的操作数。基于这种原理的反调试技术称为“0xCC探测技术”。
在2.1.3中我们介绍了API HOOK,其中提到HOOK代码可以通过检查HOOK点是否原API指令来检测HOOK实现反调试。API断点的检测原理和检测HOOK代码相同,API断点一般下在API的首地址处或函数返回地址处。所以检测这些易被下断的地址首字节是否为0xCC即可判断程序是否正在被调试。

破解方式:把断点下在函数中间,或使用硬件断点下断。
为防止调试时把断点下在函数中间,反调试程序除探测0xCC外,通常采用比较特殊代码区域(易被下断点的区域)的校验和的值。这样,在该代码区域内调试时,只要调试器在该区域内设置一些0xCC断点,如此一来,新的校验值就和原来的不一样了,这样就能判断出进程是否被调试了。
 破解方法:遇到校验和检测的时候,首选F9运行过被检测代码区,需要单步分析的时候则使用F7单步,需要步过使用硬件断点步过。也可以通过下内存访问断点,找到计算校验和代码的地方,改变比较跳转。
破解方法:遇到校验和检测的时候,首选F9运行过被检测代码区,需要单步分析的时候则使用F7单步,需要步过使用硬件断点步过。也可以通过下内存访问断点,找到计算校验和代码的地方,改变比较跳转。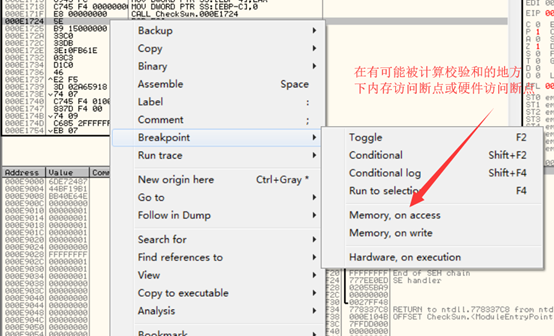
在3.3中我们知道0xCC断点容易被检测到,这时需要硬件断点来临时过渡。硬件断点的实现实际依赖于几个调试寄存器:Dr0Dr7。Dr0Dr3保存硬件断点的地址,Dr4、Dr5保留,Dr6、Dr7用于说明哪个硬件断点触发的相关属性。所以同时最多能设置4个硬件断点。只要检查Dr0~Dr4这几个寄存器的值是否为0就知道有没有没下硬件断点、有几个硬件断点。查询调试寄存器的方式一般有两种:API直接查询寄存器的值、主动触发异常查询寄存器的值。
直接API查询寄存器的值:
破解方式:修改参数中context.ContextFlags的值,或HOOK GetThreadContext的参数值,把context.ContextFlags的值改为CONTEXT_INTEGER(0x10002)值,不让该函数查询调试寄存器的值即可。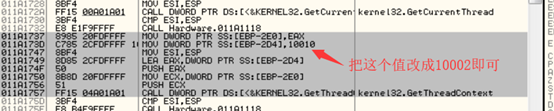
或HOOK GetThreadContext,HOOK API首地址:

注意,GetThreadContext会被系统函数调用,所以一般不要HOOK该函数,或判断调用是否来自用户代码再决定是否执行HOOK代码。
主动触发异常检查寄存器的值:
破解方法:这种反调试技术没有直接调用API而是调用SEH根据异常CONTEXT查询寄存器的值不容易被发现,特别是这个异常处理函数需要OD主动忽略异常才能传递给程序处理,这时候如果逆向分析人员没有追踪分析异常处理函数,就很容易“被反调试”。这种反调试就只能跟踪异常处理函数本身,然后在查询调试寄存器的地方改变其查询比较结果即可。
逆向分析人员在分析关键代码区的时候除了在API下断,还需要不断的单步分析,OD的F7单步步入和F8单步步过的原理就是设置单步异常或0xCC断点。反调试程序可以针对这一点设置陷阱,检测TF或0xCC实现反调试。
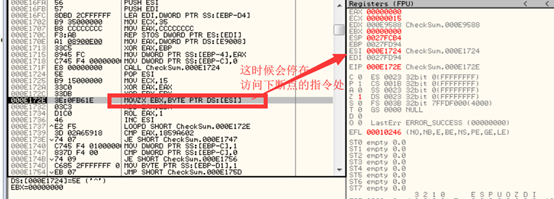
当遇到call指令或rep指令的时候,逆向人员经常会采用F8步过的方式快速步过指令执行序列。这时候,call指令或rep指令的下一条指令起始字节就会被设置一个软件断点(0xCC)。反调试程序可以在执行call指令或rep指令的时候检测下条指令是不是被下0xCC断点或直接把下条指令改成NOP指令使0xCC断点失效来实现反调试:
使0xCC断点失效原理:
当12F207B遇到rep或call习惯性F8步过的时候,12F207D的0x8B就会变成0xCC(INT3),这时rep指令或call指令会把12F207D重新恢复成原指令字节8B。这样rep或call步过后,本应断下的0xCC断点并不会断下,调试器没有重新得到控制权,程序继续执行,又得重新分析。当然这种反调试手段麻烦的一点在于重新把原字节(0x8B)写回去需要把代码段属性修改为可写。不过这种反调试手段一般在恶意代码中比较常见,而恶意代码经常申请堆内存执行恶意行为,而申请的堆内存时的属性若是可读可写可执行的,就不存在这个麻烦。
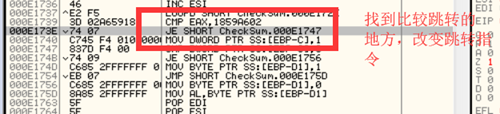
检测是否存在因调试步过而设置的0xCC断点:
这种检测rep/call步过的0xCC断点的反调试技术可以应用在任何地方。这里的例子只是为了说明其原理,实际应用实可以有多种变化。
破解方法:碰到rep或call的时候要多注意esi/edi这些敏感寄存器实际指向的地址,而且这种步过检测会有读取/写入代码区字节的行为,逆向分析遇到代码区有读取/写入行为的时候要多使用内存断点和硬件断点,尽量不用软件断点。
当EFLAGS的TF标志位被置1时,CPU将进入单步执行模式。单步执行模式中,CPU执行1条指令后即触发一个EXCEPTION_SINGLE_STEP异常,然后TF会自动清零。TF检测一般有两种和方式,第1种:主动触发TF异常、与SEH结合使用探测调试器。
破解方法:这种先pushfd修改后再popfd的方式是最常见的TF标志反调试手段,破解方法和3.2中异常处理一样,OD调试设置项就可以解决,不过需要仔细分析异常处理函数过程。
第二种检测TF的方式相反,不主动设置TF标记位,检测是否关键区有代码被单步调试:检测调试器是否在设置TF标记位。检测原理是:
但前面已经说过,当F7单步执行pushfd时,TF标志位会被自动清零,所以后面的test结果永远为0。这时候需要用到一条特殊的指令:pop ss。pop ss会将异常和中断挂起,直到下一条指令执行完毕:
单步执行pop ss时,TF异常会被挂起,执行完下一条指令才会处理TF异常,所以程序不会停在pushfd这条指令处,而是停在test指令处。
破解方法:直接运行跳过这段代码,或修改test比较结果。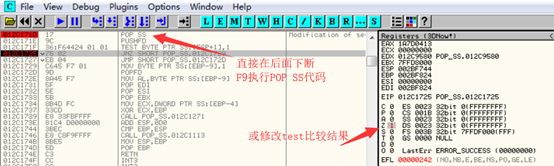
同一个进程不允许同时被两个调试器调试,利用这一点可以自己先调试运行自己,防止被另一个调试器继续调试。一般这种反调试程序会创建一个用于同步的内核对象,用第1次打开的进程主动第2次打开进程,并调试第2个进程。
进程第1次运行时会尝试访问同步内核对象,如果不存在,则说明当前进程第1次运行,创建一个内核对象,并以调试方式创建进程打开“自己”。这时若调试器首次调试运行进程则相当于在调试一个调试器,由于第2次运行的进程是被第1次运行的调试打开的,所以调试器也无法继续调试第2次运行的进程。
 破解方式:
破解方式:
1、 调试打开程序时,修改OpenXXX等打开同步对象的API返回值,使程序走正常流程。
2、 主动创建一个同名内核对象CreateXXX,使OpenXXX等打开同步对象的操作成功,走向正常流程。
这里只是简单演示这种自调试的原理,在实际逆向中,被逆向程序可能是个加密、压缩、代码被偷取等等不完整的进程,需要在第2次被自身调试打开时在调试循环中完成自修补。这样的反调试才是难对付的,大大增加了逆向分析难度。需要逆向分析人员程序的调试循环进行跟踪分析,把修补后的完整程序从内存中DUMP出来再逆向分析。
自调试除上节讲的CreateProcess()以调试方式打开进程外,还可以选择正常创建自身,然后马上附加创建进程的操作来实现。DebugActiveProcess()就可以做到这一点。
破解方式:由于这时是先创建进程再马上附加的方式实现自调试,所以除3.5.1的破解方式外,我们还可以让程序在创建自身进程后直接退出,不让其附加创建的进程,由调试器去附加。而面临的问题和3.5.1相同,自调试只是个手段,自修补才是核心,不让它自调试程序就不能补全自身,给逆向分析带来麻烦。
通过本文总结的这些反调试技术可以看出,静态反调试技术偏于“大格局”,像进程本身的一些标志位查询、调试环境检查等,动态反调试偏于“小细节”,像异常处理、断点检测等。这些技术如果只单纯应用其中的一种,其实是不难发现与破解的,但如果他们综合利用,互相隐蔽,那就大大增加了发现和破解的难度。这些反调试技术综合来说还是“死的”,弄明白原理就不难破解,所以现在的优秀反调试技术已经不局限于用这些“死板的”技术去调戏逆向分析人员了,他们开始使用像代码混淆、花指令、VMP等手段在精神上给逆向分析人员造成魔法伤害,而这种反调试手段的破解方式就是:老实逆向分析,同样的加花、混淆、VMP保护手段分析出原理了,以后就能增加魔抗、快速破解反调试手段了。所以,终级的反反调试手段还是增加自己的基本功-“他强任他强 清风拂山岗”。
另外,北京天融信阿尔法实验室常年招人,实验室专注漏洞相关技术研究,二进制和WEB方向岗位均可,诚挚欢迎各位有志从事逆向分析、样本检测、漏洞挖掘、渗透测试以及移动端安全研究相关工作的小伙伴。有兴趣的请投递简历到:http://blog.topsec.com.cn/人才招聘/
参考资料:
本文记给自己看,师傅们请移步下一篇博文,蟹蟹~
这比赛没学到啥有意义的新知识。逆向有两道题是常规题,付出一定时间大家都能做出来,还有一题全场零解,还没给提示,赛后也没wp。misc很有意思,可惜我以后不走工控安全这条路。
原本期待这个比赛好久了,想和各位师傅们同台竞技一波。结果老张同我讲话,说”组委会都决定了,你来当逆向出题人。“我说另请高明吧,我实在也不是谦虚,我一个搞逆向的菜逼怎么到出题组里来了呢?但是, 老张讲‘大家已经研究决定了。’ 所以后来我念了两首诗,叫‘+++++++,+++++++。’ 所以我就到了出题组。